If you’ve ever looked up information about rockets, chances are you’ve come across terms like G and TWR. These concepts may seem confusing at first, but we’ll explore them together to show that they are not as complicated as they might appear.
In this article, we will introduce these concepts by examining the liftoff of a rocket.
The Thrust of a rocket
A rocket moves forward by expelling gas in the opposite direction of its intended path: if it needs to go upward, it expels gas downward. You can conduct a similar experiment at home with a simple balloon: inflate the balloon and seal it with the opening facing downward. When you release the opening, the air inside the balloon is pushed downward, causing the balloon to move upward. This principle is stated by Newton’s third law.1
If the gas goes downward, it’s because a force is pushing it in that direction. According to Newton’s third law, this means an equal and opposite force is pushing the balloon in the opposite direction. In the case of a rocket, the engines push gas downward with a certain force, and this force is what we call the thrust23 of a rocket. Since thrust is a force, its unit in the International System is the Newton, denoted as N.4
From Thrust to Acceleration
We’ve established that it’s the thrust provided by the engines that enables a rocket to move forward. However, what we want to determine is how fast it can take off. It’s crucial not to confuse throwing a ball with the operation of a rocket: in predicting the motion of a thrown ball, it’s the speed at which it leaves the hand that matters, while a rocket continues to be propelled after liftoff. Therefore, instead of focusing on the rocket’s speed, we are interested in its acceleration. Here, we will once again benefit from the work of Isaac Newton, specifically his second law, which provided the modern version of the fundamental principle of dynamics: the acceleration of an object is proportional to the sum of the forces acting on it and inversely proportional to its mass. In mathematical terms, this can be expressed as:
$$
\vec{a} = \frac{1}{m} \sum_i \vec{F}_i
$$
Where \(\vec{a}\) represents the acceleration of the rocket, \(m\) is its mass, and for every \(i\), \(\vec{F}_i\) denotes a force acting on the rocket.
We will now consider the moment when our rocket lifts off from the launch pad, which is right after losing contact with the ground. At this moment, two main forces act on the rocket5: the weight of the rocket and its thrust. We assume that the rocket is perfectly vertical, so the weight and thrust are in the same direction but opposite in sense. Therefore, we can focus only on the vertical component of acceleration:
$$
a = \frac{1}{m} \left( F_p – m g \right)
$$
Where \(m\) is the mass of the rocket, \(a\) is its upward acceleration, \(F_p\) is the thrust upward, and \(g\) is the Earth’s gravity. We can also rewrite the equation in the following form :
\begin{equation}
a = g \left(\frac{F_p}{m g} – 1 \right)
\tag{AccG}\label{eq:acc_twr}
\end{equation}
Since we aim to lift off the rocket, the acceleration \(a\) must be strictly positive, meaning that the thrust \(F_p\) must be strictly greater than the weight \(m g\). In other words, their ratio must be strictly greater than \(1\) :
$$
\frac{F_p}{m g} \gt 1
$$
The TWR and the number of Gs
You’ve encountered this new term that is compared to the value 1? It’s the ratio of thrust to the weight of the rocket. We’ll call it the Thrust-to-Weight Ratio6, often abbreviated as TWR. What’s interesting is that we can now compare rocket accelerations independently of their weight: if one rocket has a TWR twice as high as that of a second rocket, then the first one will accelerate twice as fast.
If we take a closer look at equation \eqref{eq:acc_twr}, we notice that the rocket’s acceleration at sea level is equal à \(g\) times the TWP minus \(1\). This last term is present because we focused on the rocket at sea level. However, if the rocket is in space, far from any gravitational attraction (in microgravity), then the acceleration would simply be equal to the TWR times \(g\). For a rocket with a TWR of \(2\), we would say that the rocket has an acceleration of \(2 g\).
It’s worth noting that a TWR of \(1\) does not allow the rocket to ascend from sea level. However, if there were no ground, it wouldn’t fall either; it would be in perfect balance. From the passengers’ perspective, a rocket with a TWR of \(1\) is equivalent to being on the surface of the Earth. This holds true regardless of whether the rocket is near the Earth or not.7
This also means that if the TWR is \(2\), passengers will feel twice as heavy. This is not just a feeling: all mechanical structures of the equipment must also withstand this higher “apparent weight.” Therefore, there is often a desire to limit these additional mechanical stresses by restricting the TWR of spacecraft. To achieve this, it is essential to ensure that at any moment during the flight, the TWR (defined as the ratio of thrust to the weight one would feel at sea level on Earth) is below a certain threshold depending on the vehicle’s contents.
A small application?
Let’s consider a very simple vehicle with a MK1-3 command pod, a Mk16-XL parachute, a TD-25 decoupler, a Rockomax X200-16 fuel tank, and a RE-I5 Skipper engine. Additionally, three Kerbonauts will board the command pod with all the necessary equipment. We will attempt to calculate the TWR (Thrust-to-Weight Ratio) at liftoff and then the theoretically maximum achievable TWR for the spacecraft. Let’s get started!
Parameters
Before diving into the calculations, let’s first see what we need to determine this famous TWR. By definition, we’ll need to retrieve the engine’s thrust and the spacecraft’s weight.
For the thrust, the game or an online Wiki provides this information. We learn that the engine has a thrust of \(568.75\ \mathrm{kN}\) in an atmosphere with a pressure of \(1\ \mathrm{atm}\) (read as one atmosphere), corresponding to sea level on Earth or Kerbin. It’s also noted that its thrust is \(650\ \mathrm{kN}\) in a vacuum. Most rocket engines exhibit this property: they are more efficient in a vacuum than in an atmosphere, but we’ll discuss this another time.
For the weight of the spacecraft, we will only consider the gravitational acceleration at sea level on Kerbin, denoted as \(g = 9.81\ \mathrm{m/s^{2}}\). The next step is to determine the mass of the spacecraft. One could sum up the masses of the different parts of our rocket, including the mass of the Kerbonauts, but we will simply look at the mass indicated in the Vehicle Assembly Building (VAB) with the tank full and the tank empty:
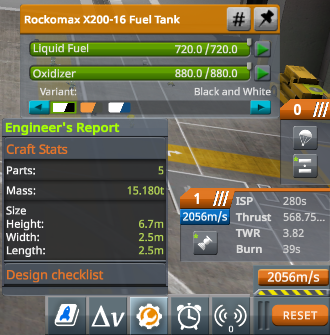
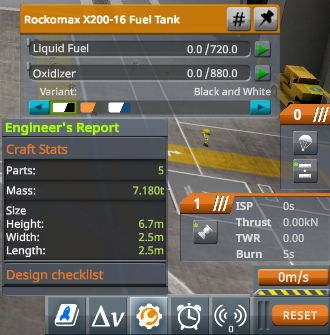
Therefore, we read that the rocket has a mass of \(15.180\ \mathrm{t}\) or \(15,180\ \mathrm{kg}\) when the tank is full, and a mass of \(7.180\ \mathrm{t}\) or \(7,180\ \mathrm{kg}\) when the tank is empty. So, we now have everything we need to proceed with the calculations!
The calculations
Let’s start by calculating the minimum TWR of the rocket when the engine is at full power. Since the TWR is defined as the ratio of thrust to weight, it is minimal when the thrust is at its lowest and the weight is at its highest, meaning the highest mass. This occurs with a thrust of \(568.75\ \mathrm{kN} = 568,750\ \mathrm{N}\) and a mass of \(15,180\ \mathrm{kg}\). Therefore, we obtain:
$$
\mathrm{RPP_{min}} = \frac{568,750}{15,180 \cdot 9.81} \approx 3.819
$$
One can indeed verify that the VAB indicates a TWR of \(3.82\), which is the rounded value of the one we have found.
It is now time to calculate the maximum TWR, which is reached when the thrust is at its maximum and the mass is at its minimum. This occurs with a thrust of \(650\ \mathrm{kN} = 650,000\ \mathrm{N}\) and a mass of \(7,180\ \mathrm{kg}\). Therefore, we obtain:
$$
\mathrm{RPP_{max}} = \frac{650,000}{7,180 \cdot 9.81} \approx 9.228
$$
As before, one can verify that the VAB indicates a TWR of \(9.23\) when the tank is nearly empty, and the engine is firing in a vacuum.
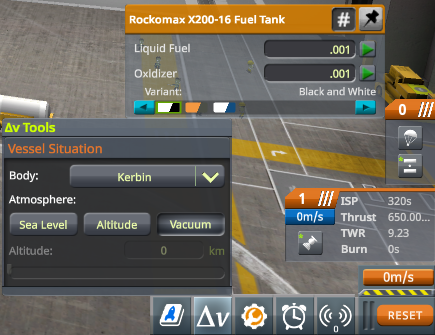
Indeed, one can conduct the experiment: on the launch pad, we observe that the displayed TWR is \(3.83\), while it reaches \(9.15\) when the tank is nearly empty. The discrepancies can be explained quite simply.
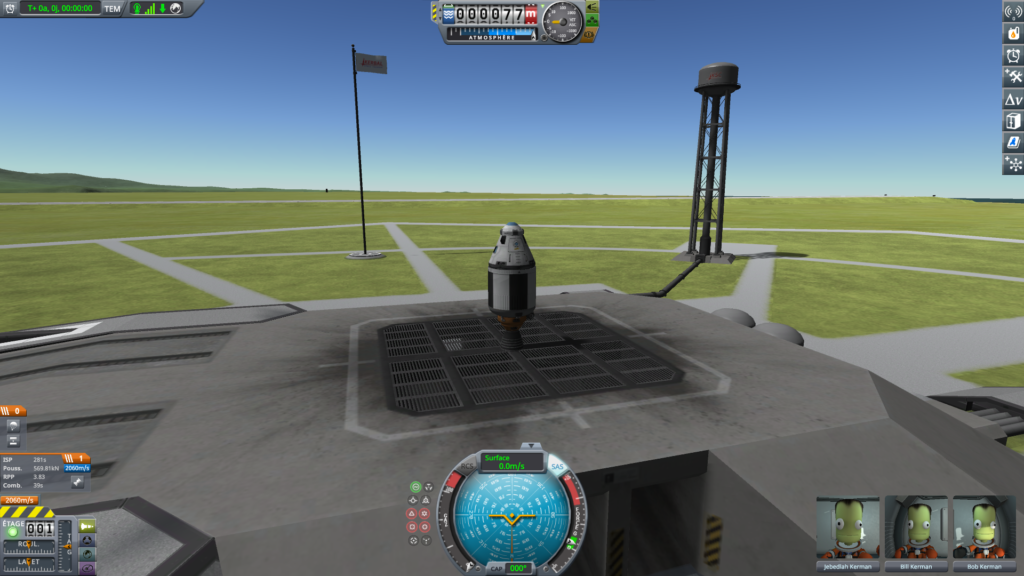
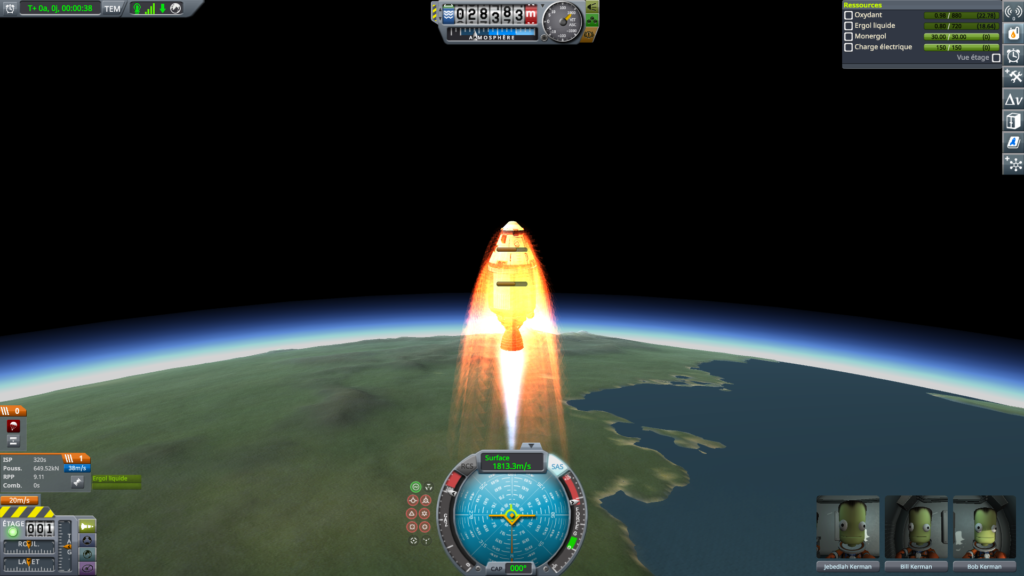
We can see that on the launch pad, the engine has an ISP8 of \(281\ \mathrm{s}\), while the Wiki indicates a sea level ISP of \(280\). We deduce that the engine on the launch pad has a slightly higher thrust than \(568.75\ \mathrm{kN}\).
The theoretical maximum TWR doesn’t seem to be reached, while the indicated ISP is. This is simply because the tank is not yet empty. Therefore, there must be around twenty kilograms of fuel left: I’ll let you do the calculation to determine it. 😉
Limit the number of Gs
We’ve seen how to calculate the thrust-to-weight ratio of a rocket based on its mass and the maximum thrust of its engines. Now, let’s focus on setting the value of the maximum TWR reached by limiting the thrust of the engines. This can be useful when one aims to transport payloads that are not very resistant to high accelerations, such as tourists.
Let’s decide to allow a maximum TWR of \(5\), which corresponds to a maximum acceleration of \(5\ g\). We will then search for a value \(\alpha\) between \(0\) and \(1\), which will indicate the limit to be applied to the engines to ensure compliance with this restriction.
We aim to limit the maximum TWR, so we consider the minimum achievable mass, i.e., \(7,180\ \mathrm{kg}\), and the maximum thrust in a vacuum, i.e., \(650,000\ \mathrm{N}\). This leads to the equation:
$$
\mathrm{RPP_{max}} = 5 = \frac{650,000 \alpha}{7180 \cdot 9.81}
$$
We can deduce the equivalent equation by multiplying by the denominator and dividing by \(650,000\):
$$
\alpha = \frac{5 \cdot 7,180 \cdot 9.81}{650,000} \approx 0.5418
$$
Therefore, the engine must be limited to \(54 \%\) of its maximum power to ensure that the spacecraft will not experience thrust exceeding \(5\ g\) during its ascent. I’ll let you try this adjustment yourself and provide your tourists with safe journeys. 🙂
Conclusion
In this article, we have explored the basic principle of thrust, its connection to rocket acceleration, \(g\) as the unit of acceleration, and the concept of the thrust-to-weight ratio.
We have also seen that we can calculate this TWR ratio based on the engine thrust and the mass of the spacecraft. Furthermore, we explored how to determine the limit to apply to the engine thrust to ensure that the spacecraft will not accelerate too strongly.
I hope you enjoyed reading this article and that it inspires you to explore further with other articles available on the website.
- https://en.wikipedia.org/wiki/Newton%27s_laws_of_motion#Third_law
- You’ll have to get used to it: scientists don’t often have much imagination when it comes to giving names.
- https://en.wikipedia.org/wiki/Rocket_engine
- https://en.wikipedia.org/wiki/Newton_(unit)
- We neglect air friction for the sake of simplicity and because the rocket has an extremely low velocity, which implies friction forces that are negligible compared to other forces.
- You’ve been warned: no imagination for coming up with original names, but at least we know what we’re talking about.
- The Einstein equivalence principle: https://en.wikipedia.org/wiki/Equivalence_principle#The_Einstein_equivalence_principle
- I promise you: we will talk about it in a future article 🙂



